1. 简介
(第1、2部分的内容比较重要,但刚开始看只需要快速过一下了解这些内容即可,与后边的例子对应起来看会比较清晰一些,从第3部分开始)
Ceres Solver是一个开源的C++库,用于建模和解决大型复杂的优化问题。它可以用于解决带有界约束的非线性最小二乘问题以及一般的无约束优化问题。比如SLAM中的优化问题,Bundle Adjustment的本质也离不开最小二乘原理,因此也可以用Ceres Solver求解。关于Ceres更多的一些特点可以参见谷歌的官方文档说明”Why?“部分。
Ceres可以用来解决如下形式的带有边界限制的非线性最小二乘法问题:
\(
\begin{eqnarray}
&\min_x\frac{1}{2}\sum_i\rho_i\left(||f_i(x_{i_1},\ldots,x_{i_k})||^2\right)\nonumber\\
&s.t.\space\space l_j\leq x_j\leq u_j\nonumber
\end{eqnarray}\tag{1}\label{1}
\)
在数据科学中的曲线拟合以及计算机视觉中的BA的核心问题都可以归结为以上形式,因此,想要使用Ceres Solver求解非线性优化问题,都需要将问题归结为以上形式。
其中,表达式\(\rho_i\left(||f_i(x_{i_1},\ldots,x_{i_k})||^2\right)\)叫做残差块ResidualBlock,其中\(f_i()\)是代价函数cost function,代价函数的值取决于优化变量\([x_{i_1},x_{i_2},\ldots,x_{i_k}]\)。在大多数的优化问题中,都是由标量组合而成的。例如平移向量由三个分量组成,一个四元数由四个分量组成,组合起来之后就可以定义运动的姿态。我们管这样的由一小簇标量组成的组叫做参数块ParameterBlock。\(l_j\)和\(u_j\)是参数块的边界,这个可以看作是状态的约束。\(\rho_i\)是一个损失函数LossFunction(也有其他文章里称为核函数),损失函数是一个标量函数,用于降低异常值对于非线性最小二乘问题的影响,比如剔除在定位过程中一些明显不正确的数据(GPS数据跳变),以避免定位误差过大。考虑一类特殊情况,当\(l_j=-\infty\), \(u_j=\infty\) 时,我们得到了无约束的非线性最小二乘问题:
\begin{eqnarray}
\min_x\frac{1}{2}\sum_i\rho_i\left(||f_i(x_{i_1},\ldots,x_{i_k})||^2\right)\nonumber
\end{eqnarray}
\)
2. 需要做什么工作?
通过上面的介绍,我们可以确定,为了使用Ceres来解决非线性优化问题,必须要确定的内容有:
- 第一步,参数块的定义(待优化变量),弄清楚待优化变量是普通的标量、向量,还是四元数、李代数等形式
- 第二步,构建代价函数
cost function或残差residual,也就是确定残差的计算形式 - 第三步,构建优化问题
ceres::Problem:通过AddResidualBlock添加残差块或者代价函数(cost function)、损失函数(loss function核函数) 和 待优化状态量 - 第四步,配置求解器(
ceres::Solver::Options),如迭代次数,终止条件等 - 第五步,运行求解器(
ceres::Solve(options, &problem, &summary))
其他一些需要关注以及可能用到的内容有:
- 定义残差计算中雅可比的计算方式(官方推荐自动求解,但有些情况下解析法计算微分,比依赖于链式法则的自动微分要更加高效)
3. 问题描述
采用g2o使用说明中相同的优化问题,简要描述如下:
假设一个机器人初始起点在0处(用\(x_0\)表示),然后机器人向前移动,通过编码器测得它向前移动了1m,到达第二个地点\(x_1\)。接着,又向后返回,编码器测得它向后移动了0.8米(用\(x_2\)表示)。但是,通过闭环检测,发现它回到了原始起点。可以看出,编码器误差导致计算的位姿和观测到有差异,那机器人这几个状态中的位姿到底是怎么样的才最好的满足这些条件呢?
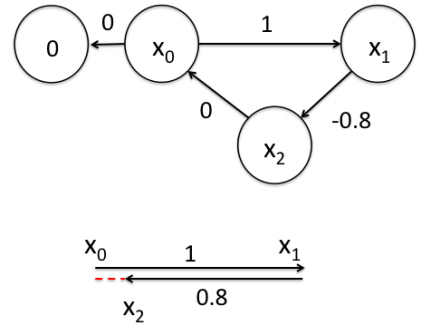
首先,机器人的位置变换了三次,即\(x_0,x_1,x_2\),其中\(x_0\)位于初始点\(0\),因此,我们把机器人的位置当做顶点,也就是\(x_0,x_1,x_2\)三个顶点。
各个顶点(位置变量)之间的约束关系定义成残差的形式可以表示为:
\(
\begin{eqnarray}f_1(x_0) &=& x_0 = 0 \tag{2.1}\label{2.1}\\f_2(x_0,x_1) &=& x_1 - x_0 - 1 = 0\tag{2.2}\label{2.2}\\f_3(x_1,x_2) &=& x_2 - x_1 + 0.8 = 0\tag{2.3}\label{2.3}\\f_4(x_0,x_2) &=& x_2 - x_0 = 0\nonumber\tag{2.4}\label{2.4}\\F(x)&=&[f_1(x),f_2(x),f_3(x),f_4(x)]\tag{2.5}\label{2.5}\end{eqnarray}
\)
其中\(F(x)\)是一个有四项参数的函数,并且有四个残差,我们希望寻找到使\(\frac{1}{2}||F(x)||^2\)最小化的\(x\),对应到ceres的标准化问题即求解\(\min_x\frac{1}{2}||F(x)||^2\)。
4. Ceres解决该优化问题
根据第2部分中说明的需要确定的内容中,第一步是确定待优化变量的形式,这里是对应了3个标量,即\(x_0,x_1,x_2\)。第二步是定义残差函数,一共有四个残差函数\(\eqref{2.1}-\eqref{2.4}\),每一个都对应一个结构体:
struct F1 {
template <typename T> bool operator()(const T* const x0,
T* residual) const {
residual[0] = x0[0];
return true;
}
};
struct F2 {
template <typename T> bool operator()(const T* const x0,
const T* const x1,
T* residual) const {
residual[0] = x1[0] - x0[0] - T(1.0);
return true;
}
};
struct F3 {
template <typename T> bool operator()(const T* const x1,
const T* const x2,
T* residual) const {
residual[0] = x2[0] - x1[0] + T(0.8);
return true;
}
};
struct F4 {
template <typename T> bool operator()(const T* const x0,
const T* const x2,
T* residual) const {
residual[0] = x2[0] - x0[0];
return true;
}
};
注意,这里给定的变量是const T* const x0,但在计算残差的时候,使用的是x0[0],因为这里给定的是一个数组。
还可以以紧凑的形式来构建,
struct CostFunctor {
template <typename T>
bool operator()(const T* const x0, const T* const x1, const T* const x2, T* residual) const {
residual[0] = x0[0];
residual[1] = x1[0] - x0[0] - T(1);
residual[2] = x2[0] - x1[0] + T(0.8);
residual[3] = x2[0] - x0[0];
return true;
}
};
当然,待优化变量也可以采用紧凑的方式,但是会导致无法设置固定点(设置不参与优化的变量),因此,这里采用散装的形式,后续示例代码中也会展示待优化变量为紧凑的形式。
第三步是构建优化问题,添加残差块,设置求导方式(自动求导),构建方式如下:
//构建优化问题
ceres::Problem problem;
//待优化变量及变量初始值
double x0 = 0;
double x1 = 1.3;
double x2 = 0.5;
// 添加残差,定义残差计算方式
// 这里采用自动求导的方式来获取导数(雅可比)
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<F1, 1, 1>(new F1),
NULL,
&x0);
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<F2, 1, 1, 1>(new F2),
NULL,
&x0, &x1);
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<F3, 1, 1, 1>(new F3),
NULL,
&x1, &x2);
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<F4, 1, 1, 1>(new F4),
NULL, ^ ^ ^
&x0, &x2); | | |
| | |
residual的维度----- + | |
变量x0的维度------------+ |
变量x2的维度---------------+
需要注意的是括号<F2, 1, 1, 1>里面的参数顺序,第一个参数为残差结构体,第二个参数为residual变量的维度,然后才是待优化变量的维度。
同样,也可以写成紧凑的形式:
// 添加约束
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<CostFunctor, 4, 1, 1, 1>(new CostFunctor),
nullptr,
&x0, &x1, &x2
);
里面参数的顺序和散装的形式相同,第一个参数为残差结构体,第二个参数为residual变量的维度,然后是各个待优化变量的维度。
第四步是配置求解器
ceres::Solver::Options options; ceres::Solver::Summary summary;//求解过程信息 options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY; // 可选设置项,增量方程如何求解 options.minimizer_progress_to_stdout = true; //可选设置项,输出到cout options.max_num_iterations = 20; //可选设置项,设置最大迭代次数
第五步,运行求解器,并输出相关优化信息及优化后的变量值
ceres::Solve(options, &problem, &summary); std::cout << summary.FullReport() << std::endl;//输出优化过程信息 std::cout << "x0: " << x0 << ", x1: " << x1 << ", x2: " << x2 << std::endl;
到这里,这个机器人定位优化问题代码框架基本上就搭建好了。
这样可以得到最终优化求解的结果为:
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time 0 1.700000e-01 0.00e+00 8.00e-01 0.00e+00 0.00e+00 1.00e+04 0 1.81e-05 1.41e-04 1 6.666686e-03 1.63e-01 8.66e-05 5.67e-01 1.00e+00 3.00e+04 1 7.51e-05 2.86e-04 2 6.666667e-03 1.92e-08 1.61e-08 3.75e-04 1.00e+00 9.00e+04 1 1.10e-05 3.12e-04 solve time cost = 0.000343761 seconds. Ceres Solver Report: Iterations: 3, Initial cost: 1.700000e-01, Final cost: 6.666667e-03, Termination: CONVERGENCE x0: 4.79467e-08, x1: 0.933333, x2: 0.0666667
5. 优化结果对比
到这里,我们就可以针对采用不同优化库得到的结果做一个对比,g2o和ceres两者的差异有两方面:
- 优化结果不同
- 优化时间差异
采用g2o优化得到的优化结果为estimated model: 0 0.933333 0.0666667 ,与ceres不同之处在于x0的取值,原因也比较明显,就是在g2o中我们将x0点设置为固定点,不参与优化,在ceres中实际上也可以做这个设置,在添加好残差项之后设置参数块为常值,设置方法如下:
problem.SetParameterBlockConstant(&x0);
再运行程序可以得到另外一个优化结果,明显,变量x0就在优化过程中保持不变为0,但是x1和x2的值也发生了变化。
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time 0 1.700000e-01 0.00e+00 5.00e-01 0.00e+00 0.00e+00 1.00e+04 0 1.19e-05 1.62e-04 1 6.666673e-03 1.63e-01 8.67e-05 5.68e-01 1.00e+00 3.00e+04 1 7.30e-05 2.98e-04 solve time cost = 0.000351709 seconds. Ceres Solver Report: Iterations: 2, Initial cost: 1.700000e-01, Final cost: 6.666673e-03, Termination: CONVERGENCE x0: 0, x1: 0.933411, x2: 0.0667489
从时间上来说,g2o的优化耗时为solve time cost = 0.000384255 seconds. ,ceres耗时为solve time cost = 0.000351709 seconds ,优化耗时差别不太大,但考虑到g2o采用的是解析法求导,ceres采用的自动求导。为了更好的比较,我们考虑把ceres优化也采用解析法求导。
6. 解析法求导
在这种情况下,需要自行提供残差和雅可比的计算方式代码,以\(f_2(x_0,x_1)\)为例,
/*
* @解析法求解雅可比
*
* param[0][0] = x0
* param[1][0] = x1
*
* | f2 |
*------|------------|
* x0 | df2/dx0 |
* | |
* x1 | df2/dx1 |
* | |
*
* jacobians[0][0] = df1/dx0
* jacobians[1][0] = df1/dx1
*
* */
class QuadraticCostFunction2 : public ceres::SizedCostFunction<1, 1, 1>{
public:
virtual ~QuadraticCostFunction2() {}
virtual bool Evaluate(double const* const* param,
double* residuals,
double** jacobians) const {
double x0 = param[0][0];
double x1 = param[1][0];
residuals[0] = x1 - x0 - 1;
if(jacobians != nullptr && jacobians[0] != nullptr){
jacobians[0][0] = -1;//残差对于x0的导数
}
if(jacobians != nullptr && jacobians[1] != nullptr){
jacobians[1][0] = 1;//残差对于x1的导数
}
return true;
}
};
这里面比较难理解的应该是<1,1,1>这几个参数和param和jacobians变量的索引。对于参数设置<1,1,1>:一开始代价函数中这几个参数我设置为<1,2>,因为考虑到param是2维的,结果运行报错: [problem_impl.cc:286] Check failed: num_parameter_blocks == cost_function->parameter_block_sizes().size() (2 vs. 1) ,问题在于 parameter_block_sizes 只有1个,而我们需要2个,也就是对应到每个残差方程里面变量的个数,我们可以通过读SizedCostFunction源码发现,模版定义为template<int kNumResiduals, int ... Ns>,构造函数为
set_num_residuals(kNumResiduals);
*mutable_parameter_block_sizes() = std::vector<int32_t>{Ns...};
因此从第2个模板参数开始,有几个参数就对应parameter_block_sizes,所以继承自SizedCostFunction类时,需要将变量的参数设置为SizedCostFunction<1, 1, 1> 。
对于SizedCostFunction::Evaluate(double const param, double* residuals, double** jacobians)函数中的param、residuals和jacobians三个变量的定义方式,根据官方文档中的说明,结合\(f_2(x_0,x_1)\)的残差定义,对各个参数说明如下:
param: 输入参数块,是一个大小为SizedCostFunction::parameter_block_sizes_.size()的数组,在\(f_2(x_0,x_1)\)的残差定义中就是依赖2个参数块(\(x_0\)和\(x_1\)),也就是存在param[0]和param[1]两个数组,param[i]是一个大小为parameter_block_sizes_[i]的数组,我们知道2个参数块(\(x_0\)和\(x_1\))都是1维的,两个数组的大小parameter_block_sizes_[1]和parameter_block_sizes_[2]的值都是1,也就是说param[0]和param[1]两个数组都是1维的。QuadraticCostFunction2依赖\(x_0\)和\(x_1\)两个参数块,那用到的参数就是param[0][0]和param[1][0]。param不会为nullptrresiduals: 是一个大小为num_residuals_(输出残差的个数)的数组,在\(f_2(x_0,x_1)\)的残差定义中为1。residuals也不会为nullptrjacobians: 是一个大小为CostFunction::parameter_block_sizes_.size()的数组,在\(f_2(x_0,x_1)\)的残差定义中jacobians就是一个2维的数组,也就是有jacboians[0]和jacboians[1]两个量。当然,如果jacobians是nullptr,用户只需要计算残差jacobians[i]: 是一个大小为 \(\mbox{num_residuals} \times \mbox{parameter_block_sizes_}[i]\) 的行数组,在\(f_2(x_0,x_1)\)的残差定义中就是\(1\times 1=1\),如果jacobians[i]不为nullptr,用户需要计算残差向量关于param[i]各个分量的雅可比矩阵,并将其存储在这个数组中,即
\mbox{jacobians}[i]\left[r\space *\space\mbox{parameter_block_sizes_}[i]+c\right]=\frac{\partial\mbox{residuals}[r]}{\partial\mbox{param}[i][c]}\tag{3}\label{3}
\)
- 在\(f_2(x_0,x_1)\)的残差定义中就是分别计算\(i=0,1\)、\(r=0\)、\(c=0\)条件下的雅可比矩阵,分别为
jacobians[0][0*1+0]和jacobian[1][0*1+0],正好对应到上边的代码中jacobians[0][0]和jacobians[1][0]的计算。 - 如果
jacobians为nullptr,通常我们只需要在Evaluate函数中实现residuals的计算,jacobians后面可以通过Ceres提供的自动求导(数值求导)替代,否则,还需要在Evaluate函数中实现jacobians的计算。 - 如果
param大小和residuals大小在编译时是已知的,就可以使用SizeCostFunction,该函数可以将param大小和residuals大小设置为模板参数,用户只需要在使用的时候给模板参数赋值就可以
以上就是解析法求导的残差定义和雅可比矩阵的求导,然后就需要将这些内容添加到ceres::Problem中,
ceres::CostFunction* F2 = new QuadraticCostFunction2;
problem.AddResidualBlock(F2,
NULL,
&x0, &x1);//注意参数块的添加方式,仍然是各参数块分别添加
problem.SetParameterBlockConstant(&x0);//这种形式仍然可以设置固定点
这样可以得到最终优化求解的结果为:
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time 0 1.700000e-01 0.00e+00 5.00e-01 0.00e+00 0.00e+00 1.00e+04 0 7.87e-06 8.77e-05 1 6.666673e-03 1.63e-01 8.67e-05 5.68e-01 1.00e+00 3.00e+04 1 4.32e-05 1.73e-04 solve time cost = 0.000203729 seconds. Ceres Solver Report: Iterations: 2, Initial cost: 1.700000e-01, Final cost: 6.666673e-03, Termination: CONVERGENCE x0: 0, x1: 0.933411, x2: 0.0667489
解析法下求导的优化问题同样可以以紧凑的形式来构建,
/*
* @解析法求解雅可比矩阵
*
* param[0][0] = x0
* param[1][0] = x1
* param[2][0] = x2
*
* | f1 | f2 | f3 | f4
*------|------------|------------|-----------|-----------
* x0 | df1/dx0 | df2/dx0 | df3/dx0 | df4/dx0
* | | | |
* x1 | df1/dx1 | df2/dx1 | df3/dx1 | df4/dx1
* | | | |
* x2 | df1/dx2 | df2/dx2 | df3/dx2 | df4/dx2
*
* jacobians[0][0] = df1/dx0
* jacobians[0][1] = df2/dx0
* .....
* jacobians[1][0] = df1/dx1
* .....
* jacobians[2][3] = df4/dx2
* */
class QuadraticCostFunction : public ceres::SizedCostFunction<4, 1, 1, 1>{//注意这里的参数
public:
virtual ~QuadraticCostFunction() {}
virtual bool Evaluate(double const* const* param,
double* residuals,
double** jacobians) const {
double x0 = param[0][0];
double x1 = param[1][0];
double x2 = param[2][0];
residuals[0] = x0;
residuals[1] = x1 - x0 - 1;
residuals[2] = x2 - x1 + 0.8;
residuals[3] = x2 - x0;
if(jacobians != nullptr){
if(jacobians[0] != nullptr){
jacobians[0][0] = 1; // df1/dx0
jacobians[0][1] = -1; // df2/dx0
jacobians[0][2] = 0; // df3/dx0
jacobians[0][3] = -1; // df4/dx0
}
if(jacobians[1] != nullptr){
jacobians[1][0] = 0; // df1/dx1
jacobians[1][1] = 1; // df2/dx1
jacobians[1][2] = -1;
jacobians[1][3] = 0;
}
if(jacobians[2] != nullptr){
jacobians[2][0] = 0; // df1/dx2
jacobians[2][1] = 0;
jacobians[2][2] = 1;
jacobians[2][3] = 1;
}
}
return true;
}
};
这里主要的问题就是弄清楚参数块\(x_0,x_1,x_2\)、残差计算residuals和雅可比矩阵jacobians的索引号,在上述代码和之前的说明中已经比较清楚了。
将残差项添加到ceres::Problem中,
ceres::CostFunction* F1 = new QuadraticCostFunction;
problem.AddResidualBlock(F1,
NULL,
&x0,&x1,&x2);
运行优化程序,得到的优化结果是相同的。
当然,待优化变量也可以采用紧凑的方式,但是同样会导致无法设置固定点(设置不参与优化的变量),代码如下,雅可比矩阵的索引号根据\(\eqref{3}\)计算确定即可。
class QuadraticCostFunction : public ceres::SizedCostFunction<4, 3>{//注意这里的参数
public:
virtual ~QuadraticCostFunction() {}
virtual bool Evaluate(double const* const* param,
double* residuals,
double** jacobians) const {
double x0 = param[0][0];
double x1 = param[0][1];
double x2 = param[0][2];
residuals[0] = x0;
residuals[1] = x1 - x0 - 1;
residuals[2] = x2 - x1 + 0.8;
residuals[3] = x2 - x0;
if(jacobians != nullptr){
if(jacobians[0] != nullptr){
jacobians[0][0] = 1; // 索引号的确定
jacobians[0][1] = 0;
jacobians[0][2] = 0;
jacobians[0][3] = -1;
jacobians[0][4] = 1;
jacobians[0][5] = 0;
jacobians[0][6] = 0;
jacobians[0][7] = -1;
jacobians[0][8] = 1;
jacobians[0][9] = -1;
jacobians[0][10] = 0;
jacobians[0][11] = 1;
}
}
return true;
}
};
什么情况下需要使用解析法求微分呢?按照官方说明,以下情况可以使用解析求导
- 函数式简单,便于求出导数解析式
- 能使用
MatlabMapleMathmaticSymPy等数学软件求出了导数的解析式 - 性能极致要求
- 没有其他好的方法去求导
- 喜欢手算导数
7. 代码
本篇对应代码项目为:
git clone https://gitee.com/mazhg/ceres_learning.git
代码目录结构为
├── cereSimpleTest.cpp //自动求导,散装优化问题 ├── cereSimpleTestCompact.cpp //自动求导,残差紧凑形式 ├── cereSimpleTestVarCompact.cpp //自动求导,残差紧凑形式,待优化变量也是紧凑形式 ├── cereSimpleTest_analytic.cpp //解析求导,散装优化问题 ├── cereSimpleTest_analytic_Compact.cpp //解析求导,残差紧凑形式 ├── cereSimpleTest_analytic_Var_Compact.cpp //解析求导,残差紧凑形式,待优化变量也是紧凑形式 ├── cmake │ ├── CeresConfig.cmake.in │ └── FindG2O.cmake └── CMakeLists.txt